Math & Music I : ความพันผูกระหว่างคณิตศาสตร์กับดนตรี
หากจะมีการพูดถึงคณิตศาสตร์กับดุริยางคศาสตร์หลายคนคงไม่คาดคิดว่าจะมีความเกี่ยวข้องกัน แต่ถ้าจะพูดถึงการทำงานของสมองที่ใช้ในการบ่มเพาความคิดในศาสตร์ทั้งสองแล้วก็ยิ่งแตกต่างกันมากขึ้นไปอีก เนื่องจากในการทำงานของสมอง เราใช้สมองซีกซ้ายในการคิดและการให้เหตุผลคณิตศาสตร์ ส่วนสมองซีกขวานั้น ทำงานในเรื่องของจินตนาการดนตรี ศิลปะ
แล้วเหตุใดศาสตร์ทั้งสองซึ่งทำงานดังเส้นขนานจะมาบรรจบกันได้เมื่อกล่าวถึงดนตรี สิ่งที่เราจะหลีกหนีไม่ได้ คือเรื่องตัวโน้ต ซึ่งเรารู้จักโน้ตหลัก 7 ตัว คือโด (C) เร (D) มี (E) ฟา (F) โซ (G) ลา (A) ที (8) กันดีอยู่แล้ว แต่ตัวโนัตสากลที่ใช้กันทุกวันนี้มีอีก 5 ตัว คือ โดซาร์ป (C#) หรือเรแฟลต (Db) เรซาร์ป (D#) หรือมีแฟลต (Eb) ฟาซาร์ป (F#) หรือโซแฟลต (Gb) โซซาร์ป (G#) หรือลาแฟลต (Ab) และลาชาร์ป (A#) หรือที่แฟลต (B)) ดังนั้นเมื่อนำน้ต 5 ตัวนี้มารวมกับตัวโน้ตหลัก ก็จะมีตัวโน้ตทั้งหมด 12 ตัว ดังภาพ โดยโน้ตที่อยู่ติดกันจะมีระดับเสียงห่างกันอยู่ครึ่งเสียง
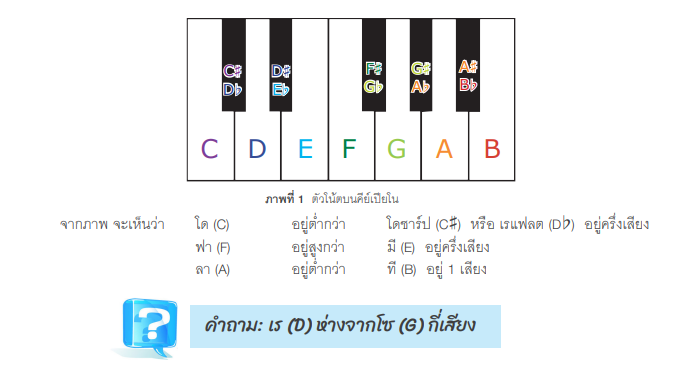
ชุดของตัวโน้ตหลัก 7 ตัวที่เรารู้จักนั้น เมื่อนำมาเรียงต่อกันเป็น ใด (C) - เร (D) - มี (E) - ฟา (F) -โซ (G) - ลา (A) - ที (B) -โด (C เรียกว่า "บันไดเสียง C เมเจอร์ (C major scale)" และเมื่อพิจารณาความห่างของโน้ตแต่ละคู่ที่อยู่ติดกันในบันไดเสียงดังกล่าว โดยพิจารณาเทียบกับภาพที่ 1 จะได้แผนภาพดังต่อไปนี้

ภาพที่ 2 ความห่างของโน้ตในบันไดเสียง C เมเจอร์
สำหรับสเกลในตระกูลเมเจอร์ หรือบันไดเสียงเมเจอร์ (major scale) ประกอบด้วยโน้ตที่แตกต่างกัน 7 ตัว ส่วนโน้ตตัวที่ 8 จะเป็นโน้ตตัวเดียวกับโน้ตตัวที่ แต่มีเสียงที่สูงขึ้ด้วยความถี่เป็นสองเท่ เราเรียกความห่างของระดับเสียงของโน้ตตัวที่ 1 และ 8 นี้ว่า "ระยะช่วงคู่แปด (Octave)" ซึ่งโน้ตแต่ละคู่ในบันไดเสียงเมเจอร์จะห่างกันดังแบบรูปต่อไปนี้

เมื่อประมาณ 5 ศตวรรษก่อนคริสตกาล พี่ทาโกรัสแห่งซามอส (Pythagoras of Samos) นักปราชญ์ชาวกรีกเป็นบุคคลที่ได้รับกรยอมรับว่าเป็นปราชญ์ที่มีความรอบรู้ทั้งด้านคณิตศาสตร์ ดาราศาสตร์ และดนตรี ทั้งยังเป็นผู้ก่อตั้ง "สำนักพีทาโกเรียน" เป็นสถานศึกษาศาสตร์ต่าง ๆ ตามแนวคิดของเขา โดยเขาและเหล่าศิษย์เป็นผู้ที่คั้นพบพีทาโกเรียนสเกล (Pythagorean scale) จากการได้ยินเสียงของเหล็กที่ตีกระทบทั่ง แล้วนำมาผนวกกับความรู้คณิตศาสตร์จนได้บันไดเสียงขึ้นมา ซึ่งต่อมาจึงได้พบว่าพีทโกเรียนสเกลและบันไดเสียงเมเจอร์เป็นบันไดเสียงที่มีความห่างของตัวโน้ตในแบบรูปเดียวกันคือ
![]()

Pythagoras of Samos
ประมาณ 580-496 ปีก่อนคริสต์ศักราช
นอกจากนี้ เราก็ยังพบอีกว่ากลุ่มของตัวโน้ต หรือคอร์ด (chord) มีความเกี่ยวพันกับจำนวนที่ได้จากทฤษฎีบทพีทาโกรัส คือ "In a right-angled triangle the square described on the hypotenuse is equal to the sum of the squares described on the other two sides."
สำหรับรูปสามเหลี่ยมมุมฉากใด ๆ พื้นที่ของรูปสี่เหลี่ยมจัตุรัสบนต้านตรงข้ามมุมฉาก จะเท่ากับผลบวกของพื้นที่ของรูปสี่เหลี่ยมจัตุรัสบนด้านประกอบมุมฉาก หรือจากภาพที่ 3 จะได้ว่า c2 = a2 + b2 ซึ่งความสัมพันธ์นี้เป็นที่รู้จักกันในนาม "ทฤษฎีบทพีทาโกรัส" มานานกว่า 2,500 ปี จากทฤษฎีบทพีทาโกรัส เราจะพบว่ามีชุดของจำนวนเต็มที่แทน a b และ c ได้หลายชุด เช่น
3, 4 และ 5
6, 8 และ 10
8, 15 และ 17
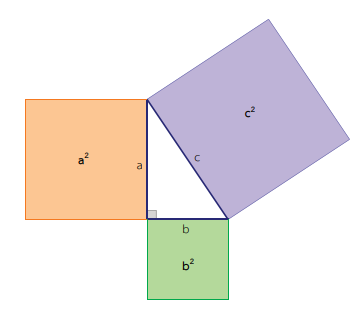
ภาพที่ 3 แสดงพื้นที่ของรูปสี่เหลี่ยมจัตุรัสบนด้านต่าง ๆ ของรูปสามเหลี่ยมมุมฉาก
และเมื่อนำชุดจำนวนดังกล่าวมาใช้ในการนับเพื่อหากลุ่มของตัวโน้ต จะทำให้ได้กลุ่มของตัวโน้ตที่เวลาบรรเลงจ0ะมีความไพเราะซึ่งลำดับของการนับสามารถเริ่มได้ที่จำนวนเต็มแทนความยาวของด้านประกอบมุมฉากด้านใดก่อนก็ได้เช่นถ้าใช้ชุดของจำนวน 3. 4 และ 5 การนับเพื่อหากลุ่มของตัวโน้ตก็สามารถทำได้ดังนี้

กลุ่มของตัวโน้ตที่หได้จากวิธีการดังกล่าวสอดคล้องกับกลุ่มของตัวโน้ตที่เรียกว่า คอร์ดเมเจอร์ (major chord) และ คอร์ดไมเนอร์ (minor chord ในดนตรีตะวันตกดังนี้
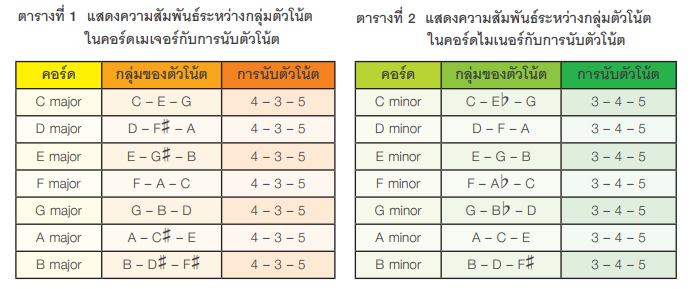
จากตารางทั้งสอง จะเห็นได้ว่ากลุ่มตัวโน้ตในคอร์ดเมเจอร์ห่างกัน 4. 3 แล: 5 ตัวโน้ต ส่วนคอร์ดไมเนอร์มีตัวโน้ตห่างกัน 3. 4 และ 5 ตัวโน้ต ซึ่งสอดคล้องกับชุดของจำนวนที่ได้จากทฤษฎีบทพีทโกรัส นอกจากนี้ ชุดของจำนวนอื่น ๆ ที่ได้จากทฤษฎีบทพีทาโกรัสก็สามารถนำมาใช้นับเพื่อหากลุ่มของตัวโน้ตได้เช่นกัน ซึ่งจะทำให้เป็นคอร์ดในกลุ่มอื่น ๆที่นอกเหนือจากคอร์ดเมเจอร์และคอร์ดไมเนอร์
จากที่ได้กล่าวมานี้ คงพอจะทำให้เห็นความสัมพันธ์ระหว่างศาสตร์ของจำนวน ในมุมของการใช้แบบรูปและชุดของจำนวนที่ได้จากทฤษฎีบทพีทโกรัสว่าเชื่อมโยงกับบันใดเสียงเมเจอร์ คอร์ดเมเจอร์ และคอร์ดไมเนอร์ ถ้าปราศจากการสังเกตและความรอบรู้ของนักปราชญ์ในศาสตร์ทั้งสองแล้ว คงเป็นเรื่องยากที่เราจะได้เห็นความพันผูกของสองศาสตร์นี้จึงเปรียบเสมือนของสองสิ่งที่เกิดขึ้นโดยธรรมชาติ แต่เรามิได้ตระหนักรู้ในความสัมพันธ์ของทั้งสองสิ่งนั้นดังเช่นคำกล่าวของนักคณิตศาสตร์ซาวเยอรมัน กอทท์ฟรีด วิลเฮล์ม ไลบ์นิทซ์ (Gottried Wihelm Leibniz, ค.ศ. 1646-1716) ที่ว่า ดนตรีคือความสำราญ ที่สั่งสมความรู้สึกนึกคิดของมนุษย์จากการนับ โดยมีได้ตระหนักว่ามันคือการนับ

บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://magazine.ipst.ac.th/
บรรณานุกรม
Akiyama.J. (2552).หนึ่งวันผจญภัยในดินแนคณิตศาสตร์มหัศจรรย์. แปลโดย จิณดิษฐ์ ะออปักษิณ และรตินันท์ บุญเคลือบ.กรุงเทพมหานคร: สาราเด็ก.
Fauvel, J. Flood, R. & Wilson. R. (2006). Music and mathematics from Pythagoras to fractals. New York: Oxford University Press.
Hall, H. S. & Stevens. F. H. (1958). A school geometry part /-V. 2nd ed. London: Macmillan & co.. Itd.
Loy, D. G. (2006). Musimathics : The mathematics foundations of music volume 1. USA: Interactive composition.
Walsh, T. P. (2010). Mathematics and music. Educating the creative mind conference 2010, 90-92. Conference proceedings of Kean University.
ณัชชา โสคติยานุรักษ์. (2546). ทฤษฎีดนตรี. พิมพ์รั้งที่ 4. กรุงเทพมหานคร: จุฬาลงกรณ์มหาวิทยาลัย.
ราชบัณฑิตยสถาน.. (2553). พจนานุกรมศัพท์คณิตศาสตร์ ฉบับรชบัณฑิตยสถาน. พิมพ์ครั้งที่ 10. กรุงเทพมหานคร: นานมีบุ๊คส์พับลิเคชั่นส์.
ความคิดเห็น
แสดงความคิดเห็น